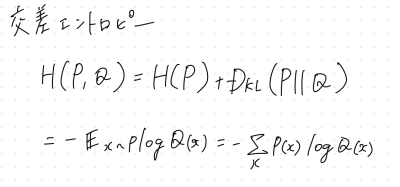■応用数学要点まとめ
第1章:線形代数
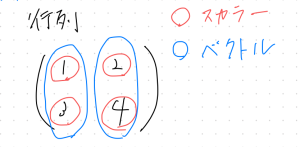
スカラーとベクトル
スカラーは、普通の1や2などの数、ベクトルは、
スカラーを複数セットで表示され、大きさと向きを持つ
行列
スカラーを表にしたもの、ベクトルを並べたもの。
行列は、ベクトルの向きや大きさを変えるための係数として扱う。
行列の積
各行×各列で新しい行列の成分を求める。
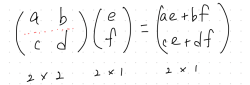
行列の積で、連立方程式をシンプルに表現できる。
また、行基本変形により、方程式を求めることができる。
★図4
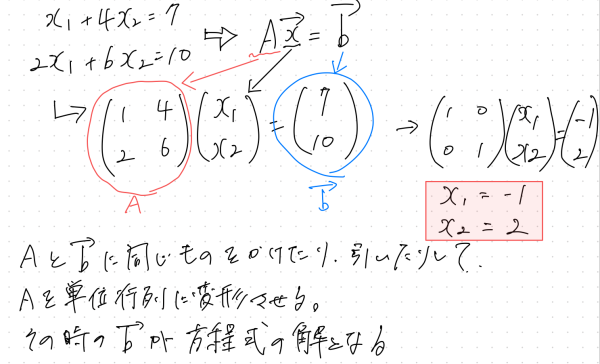
逆行列
行列Aに行列Xをかけたら、単位行列Iとなる行列Xを行列Aの逆行列という。
Aインバースと表現する。

逆行列の求め方
掃き出し法

逆行列が存在しない行列の条件がある。

行列式
例えば、2×2の行列が横ベクトルの組み合わせと考えたとき
そのベクトルで作られた平行四辺形の面積が逆行列の有無を判別する。
(面積が0の場合は逆行列が存在しない)
この面積の表現を行列式と呼ぶ
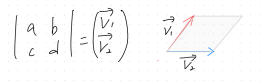
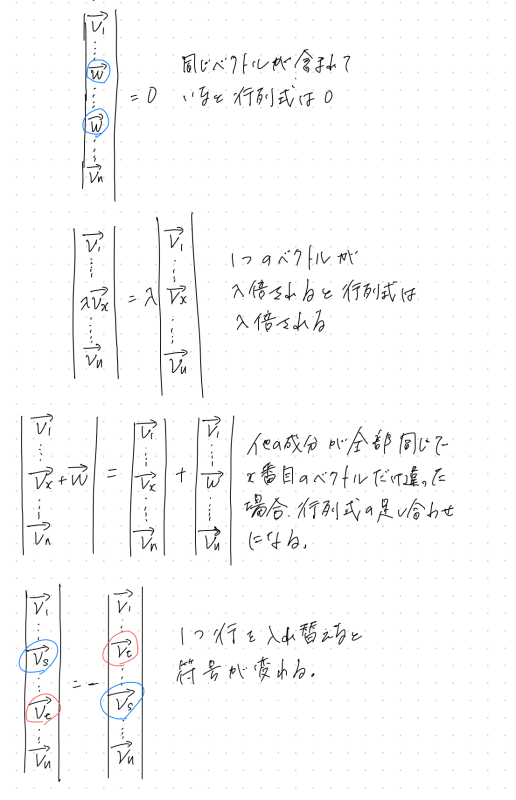
行列式の特徴
固有値

固有値、固有ベクトルの求め方
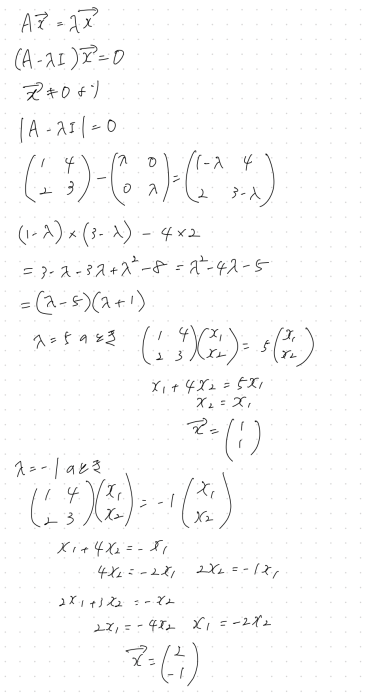
固有値分解

特異値分解
正方行列以外でも固有値分解のようなことができる。
Sはシグマをあつめた行列
U,Vは直行行列
特異値分解は、
特異値分解をした結果かから、小さい値を取り除くことにより、
画像のデータ量を小さくできる。

第2章:確率・統計
確率は大きく
頻度確認
ベイズ確認
に分けられる。
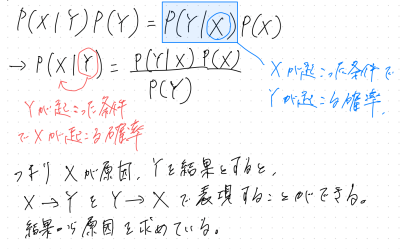
条件付き確率
ある事象X与えられた下で,Yとなる確率

独立した事象の同時確率
![]()
ベイズ則
確率変数と確率分布
確率変数:事象そのもの(さいころの目がでる確率を計算する場合は、出た目のこと)
確率分布:事象が発生する確率の分布
期待値
確率変数×確率 を足し合わせたもの

分散
データの散らばり具合
どれだけ期待値からずれているかを平均したもの
結果の確率から期待値を引いたものを2乗したもの

共分散
2つのデータの傾向の違いを表す
正の値は、似た傾向
負の値は、逆の傾向
ゼロは関係性が乏しい
2つの分散の平方根(標準偏差)の値をかけたもの

標準偏差
分散の平方根(ルート)の値
分散は2乗しているので単位が違ってしまうので
単位を元に戻したもの

様々な確率分布
ベルヌーイ分布
コイントスのイメージ
マルチヌーイ分布や2項分布、ガウス分布などがある。

第3章:情報理論
情報を数量化する
自己情報量
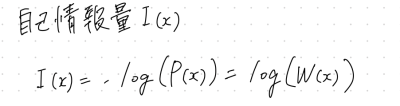
シャノンエントロピー
自己情報量の期待値

カルバック・ライブラーダイバージェンス
同じ事象・確率変数における異なる確率分布P,Qの違いを表す
例えば、あるコインを投げた確率分布と違うコインを投げた場合の
確率分布の違いを見る場合など
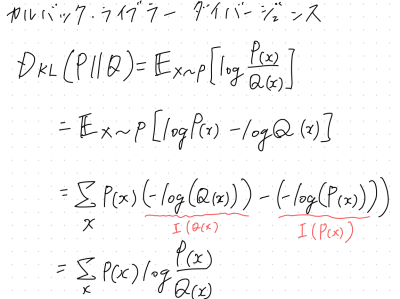
交差エントロピー
KLダイバージェンスの一部分を取り出したもの
Qについての自己情報量をPの分布で平均している。