■機械学習まとめ
■線形回帰モデル
1.要点のまとめ
回帰とはある入力からある出力を予測すること
教師あり学習の一つで、予測値のグラフが線形となるモデル。
説明変数が1つの場合を単回帰モデル、複数のモデルを重回帰モデルと呼ぶ。

モデルのパラメータは、最小二乗法により推定する。
最小二乗法は、学習データの平均二乗誤差を最小とするパラメータを
探す方法。
平均二乗誤差に対して、微分を行い、その値が0(グラフの傾きが0)
になるパラメータを求める。

2.実装演習キャプチャー
ボストンの住宅データセットを線形回帰で分析する。
説明変数が1つの場合
>>> from sklearn.datasets import load_boston
>>> from pandas import DataFrame
>>> import numpy as np
>>>
>>> boston=load_boston()
>>> print(boston['feature_names'])
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
>>> min(boston['target'])
5.0
>>>
>>> max(boston['target'])
50.0
>>>
>>>
>>> df=DataFrame(data=boston.data,columns=boston.feature_names)
>>> df['PRICE']=np.array(boston.target)
>>> df.head(3)
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT PRICE
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
>>>
>>> data=df.loc[:,['RM']].values
>>>
>>> data[0:5]
array([[6.575],
[6.421],
[7.185],
[6.998],
[7.147]])
>>>
>>> target=df.loc[:,'PRICE'].values
>>>
>>> target[0:5]
array([24. , 21.6, 34.7, 33.4, 36.2])
>>>
>>> from sklearn.linear_model import LinearRegression
>>> model=LinearRegression()
>>> model.fit(data,target)
LinearRegression()
>>>
>>>
#外挿にあたる[1]で予測すると-の値が出て予測ができない。
>>> model.predict([[1]])
array([-25.5685118])
>>>
>>>
>>>
>>> model.predict([[5]])
array([10.83992413])
>>>
>>> model.predict([[7]])
array([29.04414209])
>>>
>>> model.predict([[8]])
array([38.14625107])
>>>
RMが1の場合、予測結果が約-25と、ありえないマイナスの値の
結果となった。
これは外挿にあたる値のため、精度が悪くなるので、回帰問題を
解く場合は注意する必要がある。
説明変数を2つにした場合(重回帰)
>>> df[['CRIM','RM']].head()
CRIM RM
0 0.00632 6.575
1 0.02731 6.421
2 0.02729 7.185
3 0.03237 6.998
4 0.06905 7.147
>>>
>>> data2=df.loc[:,['CRIM','RM']].values
>>>
>>> target2=df.loc[:,'PRICE'].values
>>> model2=LinearRegression()
>>> model2.fit(data2,target2)
LinearRegression()
>>>
>>> model2.predict([[0.2,7]])
array([29.43977562])
>>>
>>> model2.predict([[70,7]])
array([10.94883073])
CRIMが0.2と70の場合を比べると、やはり犯罪率が
高いと安い傾向がある。
■非線形回帰モデル
1.要点のまとめ
複雑なデータ構造を線形で捉えられる場合は限られる。
非線形な構造をとらえる場合に使用する。
線形回帰モデルの入力の部分を非線形な関数に変えて非線形構造にしている。
回帰関数としては、基底関数を使う。
良く使われる基底関数として、
・多項式関数
・ガウス型基底関数
・スプライン/Bスプライン関数
がある。
未知のパラメータは線形回帰モデルと同様に、最小二乗法や最尤法により推定する。
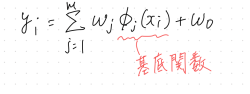
学習データに対して、十分小さな誤差が得られないモデルを「未学習」
学習データでは小さな誤差を得られるけど、テストデータでは小さな誤差を
得られないモデルを「過学習」と呼ぶ
過学習の対策
学習データの数を増やす
不要な基底関数(変数)を削除して抑止
正則化法を利用して、抑止
正則化法には、
Ridge推定、Lasso推定がある。
汎化性能
未知の入力に対する予測性能
学習データとは別に収集された検証データで性能を測る。
学習データにだけ性能が良い場合は、過学習となっている。
モデルの検証について
ホールドアウト表
データを学習用と検証用に分割し、予測精度等を推定する。
データが大量にある場合を除いては、使わないほうが良い。
データが少ない場合、検証用に分けたほうに外れ値が入ってしまうと
予測がうまくいかない。
クロスバリデーション(交差検証)
同じデータを学習用と検証用での分ける際に、分け方を変え、
それぞれの学習データ、検証データで、検証を行う方法
2.実装演習キャプチャー
線形回帰と重回帰を比較する。
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import seaborn as sns
>>> sns.set()
>>> sns.set_style("darkgrid", {'grid.linestyle': '--'})
>>> sns.set_context("paper")
>>>
>>> n=100
>>> def true_func(x):
... z = 1-48*x+218*x**2-315*x**3+145*x**4
... return z
...
>>> def linear_func(x):
... z = x
... return z
...
>>> data = np.random.rand(n).astype(np.float32)
>>> data = np.sort(data)
>>> target = true_func(data)
>>>
>>> noise = 0.5 * np.random.randn(n)
>>> target = target + noise
>>>
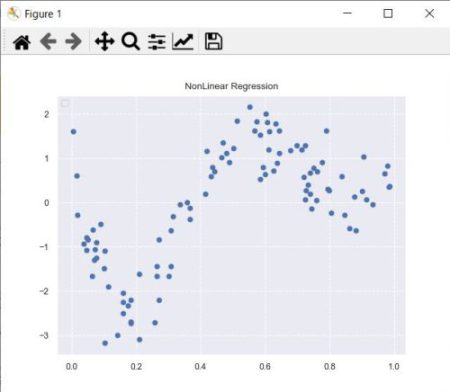
>>> plt.scatter(data, target)
<matplotlib.collections.PathCollection object at 0x0000022A7E056E80>
>>>
>>> plt.title('NonLinear Regression')
Text(0.5, 1.0, 'NonLinear Regression')
>>> plt.legend(loc=2)
No handles with labels found to put in legend.
<matplotlib.legend.Legend object at 0x0000022A7E066970>
>>>
>>> plt.show
<function show at 0x0000022A775AA5E0>
>>>
>>> plt.show()
>>>
データの散布図
>>> from sklearn.linear_model import LinearRegression
>>> clf = LinearRegression()
>>> data = data.reshape(-1,1)
>>> target = target.reshape(-1,1)
>>> clf.fit(data, target)
LinearRegression()
>>>
>>>
>>> p_lin = clf.predict(data)
>>>
>>> plt.scatter(data, target, label='data')
<matplotlib.collections.PathCollection object at 0x0000022A00005F10>
>>> plt.plot(data, p_lin, color='darkorange', marker='', linestyle='-', linewidth=1, markersize=6, label='linear regression')
[<matplotlib.lines.Line2D object at 0x0000022A00021A60>]
>>> plt.legend()
<matplotlib.legend.Legend object at 0x0000022A00021FA0>
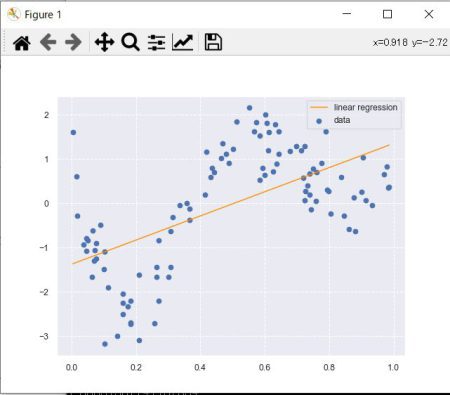
>>> print(clf.score(data, target))
0.35691937741162694
>>> plt.show()
>>>
線形回帰
曲線のデータ構造に対応できない。
重回帰(カーネルリッジ)
>>> from sklearn.kernel_ridge import KernelRidge
>>> clf = KernelRidge(alpha=0.0002, kernel='rbf')
>>> clf.fit(data, target)
KernelRidge(alpha=0.0002, kernel='rbf')
>>>
>>>
>>> p_kridge = clf.predict(data)
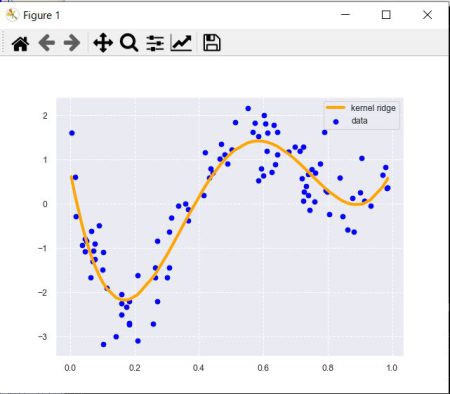
>>> print(clf.score(data, target))
0.8568319076493953
>>> plt.scatter(data, target, color='blue', label='data')
<matplotlib.collections.PathCollection object at 0x0000022A00384640>
>>>
>>> plt.plot(data, p_kridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='kernel ridge')
[<matplotlib.lines.Line2D object at 0x0000022A00393E50>]
>>> plt.legend()
<matplotlib.legend.Legend object at 0x0000022A00375670>
>>>
>>> plt.show()
曲線のデータ構造に対応できている。
■ロジスティック回帰モデル
1.要点のまとめ
教師ありの分類問題を解く手法
目的変数は、0か1の値となる。
入力とm次元パラメータの線形結合をシグモイド関数に入力する。
出力はy=1になる確率の値になる。

シグモイド関数
入力は実数で、出力は必ず0~1の値をとるので確率を表現できる。
微分をすると、シグモイド関数自身で表現することが可能
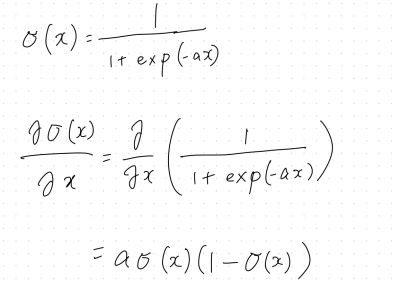
最尤推定
尤度関数を最大とするパラメータを探す
尤度関数
ある母集団(パラメータθ)から独立にn個標本を抽出した時のデータがx1,x2,....,xnの値を
とる確率は、L(θ)=f(x1,θ)f(x2,θ)....*f(xn,θ)と考えられ、
L(θ)を尤度関数という。
これが最大となるパラメータを探すことを最尤推定という。
尤度関数の対数をとると微分の計算が簡単。
対数尤度関数が最大になる点と尤度関数が最大になる点は同じ
尤度関数にマイナスをかけたものを最小化し、最小二乗法の最小化と合わせる

勾配降下法
反復学習によりパラメータを逐次的に更新していきパラメータを求める手法
対数尤度関数は、微分して0の値を探すことが難しいため、勾配降下法を使う
勾配降下法では、パラメータを更新するのにN個全てのデータに対する和を求める必要があるが、確率的勾配降下法(SGD)は、
データを一つずつランダムで選んでパラメータを
更新していく。
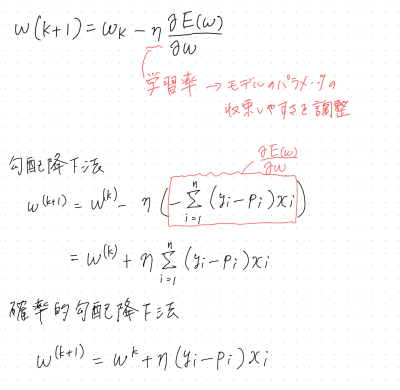
2.実装演習キャプチャー
taitanicデータを使い実装する。
>>> import pandas as pd
>>> from sklearn.linear_model import LogisticRegression
>>> titanic_df = pd.read_csv('C:/titanic_train.csv')
>>>
>>> titanic = pd.read_csv('C:/titanic_train.csv')
>>>
>>> titanic.head()
PassengerId Survived Pclass ... Fare Cabin Embarked
0 1 0 3 ... 7.2500 NaN S
1 2 1 1 ... 71.2833 C85 C
2 3 1 3 ... 7.9250 NaN S
3 4 1 1 ... 53.1000 C123 S
4 5 0 3 ... 8.0500 NaN S
[5 rows x 12 columns]
>>>
>>> titanic["AgeFill"] = titanic["Age"].fillna(titanic["Age"].mean())
>>> titanic["Gender"] = titanic["Sex"].map({"female" : 0, "male" : 1}).astype(int)
>>> X = titanic.loc[:, ["AgeFill", "Gender"]]
>>> y = titanic.loc[:, "Survived"]
>>>
>>> logistic = LogisticRegression()
>>> logistic.fit(X, y)
LogisticRegression()
>>>
>>> logistic.predict_proba([[30, 1]])
array([[0.80668102, 0.19331898]])
>>>
>>> logistic.predict_proba([[30, 0]])
array([[0.26744115, 0.73255885]])
>>>
30歳男性(約19%)と30歳女性(約74%)では、女性の方が生存率が高い。
■主成分分析
1.要点のまとめ
次元削減の手法の1つ
情報の量を分散の大きさととらえ、分散の総量が最大となる射影軸を探索する
ノルムが1となる制約を入れ最適化問題を解く
各主成分の情報の量は、寄与率や累積寄与率を用いて確認する。
寄与率
第k主成分の分散の全分散に対する割合(第k主成分が持つ情報量の割合)
累積寄与率
第1-k主成分まで圧縮した際の情報損失量の割合
2.実装演習キャプチャー
乳がんの検査データを用いて、主成分分析を実装する。
>>> import pandas as pd
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.decomposition import PCA
>>>
>>> cancer = pd.read_csv('C:/cancer.csv')
>>>
>>> X = cancer.loc[:, "radius_mean":"fractal_dimension_worst"]
>>> y = cancer.diagnosis.apply(lambda d: 1 if d == 'M' else 0)
>>>
>>>
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 5)
>>>
>>> scaler = StandardScaler()
>>> X_train = scaler.fit_transform(X_train)
>>> X_test = scaler.transform(X_test)
>>>
>>>
>>>
>>> logistic = LogisticRegression()
>>> logistic.fit(X_train, y_train)
LogisticRegression()
>>> y_pred_before = logistic.score(X_test, y_test)
>>>
>>>
>>> pca = PCA(n_components = 2)
>>> X_train = pca.fit_transform(X_train)
>>> X_test = pca.fit_transform(X_test)
>>>
>>>
>>> logistic.fit(X_train, y_train)
LogisticRegression()
>>> y_pred_after = logistic.score(X_test, y_test)
>>>
>>>
>>> "主成分分析前:{:.3f}、主成分分析後:{:.3f}".format(y_pred_before, y_pred_after)
'主成分分析前:0.979、主成分分析後:0.944'
2次元まで削減しても結果は0.35しか違わない。
■サポートベクターマシーン
1.要点のまとめ
2クラス分類問題を解く手法
回帰問題や教師無し問題へも応用されている。
どちらのクラスに属するか判定するために、決定関数が使われる。
1 or -1 を出力する。
分類境界を挟んで2つのクラスがどのくらい離れているかをマージンと呼ぶ。
マージンを最大化するパラメータを求めることにより分類する。
分離できると仮定したSVMのことをハードマージン、
分離可能でないデータに適用するものをソフトマージンと呼ぶ
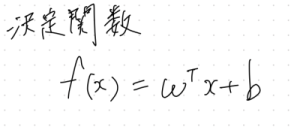
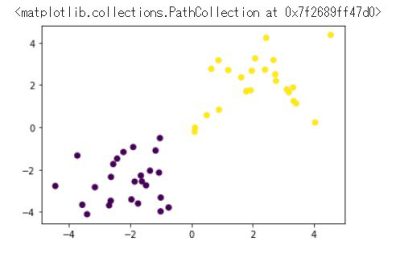
2.実装演習キャプチャー
訓練データ生成① (線形分離可能)
import numpy as np
import matplotlib.pyplot as plt
def gen_data():
x0 = np.random.normal(size=50).reshape(-1, 2) - 2.
x1 = np.random.normal(size=50).reshape(-1, 2) + 2.
X_train = np.concatenate([x0, x1])
ys_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
return X_train, ys_train
X_train, ys_train = gen_data()
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
[/st-mybox]
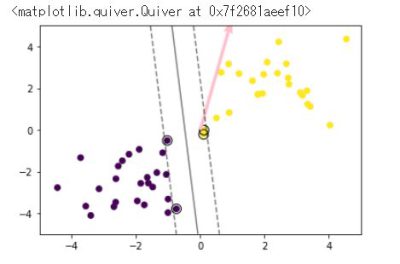
t = np.where(ys_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)
eta1 = 0.01
eta2 = 0.001
n_iter = 500
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
grad = 1 - H.dot(a)
a += eta1 * grad
a -= eta2 * a.dot(t) * t
a = np.where(a > 0, a, 0)
予測
index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()
xx0, xx1 = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)
# 訓練データを可視化
plt.scatter(X_train[:, 0], X_train[:, 1], c=ys_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
s=100, facecolors='none', edgecolors='k')
# 領域を可視化
#plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
# マージンと決定境界を可視化
plt.quiver(0, 0, 0.1, 0.35, width=0.01, scale=1, color='pink')
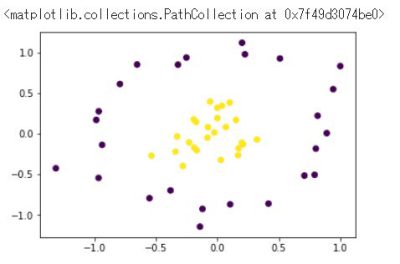
訓練データ生成② (線形分離不可能)
factor = .2
n_samples = 50
linspace = np.linspace(0, 2 * np.pi, n_samples // 2 + 1)[:-1]
outer_circ_x = np.cos(linspace)
outer_circ_y = np.sin(linspace)
inner_circ_x = outer_circ_x * factor
inner_circ_y = outer_circ_y * factor
X = np.vstack((np.append(outer_circ_x, inner_circ_x),
np.append(outer_circ_y, inner_circ_y))).T
y = np.hstack([np.zeros(n_samples // 2, dtype=np.intp),
np.ones(n_samples // 2, dtype=np.intp)])
X += np.random.normal(scale=0.15, size=X.shape)
x_train = X
y_train = y
plt.scatter(x_train[:,0], x_train[:,1], c=y_train)
学習
def rbf(u, v):
sigma = 0.8
return np.exp(-0.5 * ((u - v)**2).sum() / sigma**2)
X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# RBFカーネル
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
for j in range(n_samples):
K[i, j] = rbf(X_train[i], X_train[j])
eta1 = 0.01
eta2 = 0.001
n_iter = 5000
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
grad = 1 - H.dot(a)
a += eta1 * grad
a -= eta2 * a.dot(t) * t
a = np.where(a > 0, a, 0)
予測
index = a > 1e-6
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()
xx0, xx1 = np.meshgrid(np.linspace(-1.5, 1.5, 100), np.linspace(-1.5, 1.5, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
y_project[i] += a * sv_t * rbf(X_test[i], sv)
y_pred = np.sign(y_project)
# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
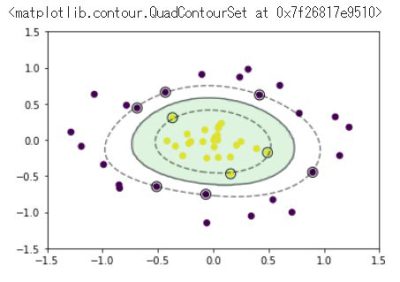
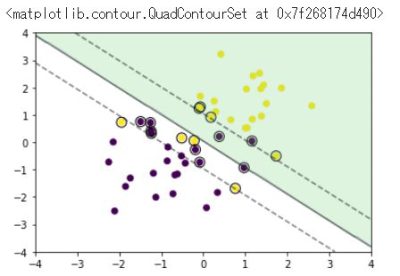
ソフトマージンSVM
訓練データ生成③(重なりあり)
x0 = np.random.normal(size=50).reshape(-1, 2) - 1.
x1 = np.random.normal(size=50).reshape(-1, 2) + 1.
x_train = np.concatenate([x0, x1])
y_train = np.concatenate([np.zeros(25), np.ones(25)]).astype(np.int)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)

学習
X_train = x_train
t = np.where(y_train == 1.0, 1.0, -1.0)
n_samples = len(X_train)
# 線形カーネル
K = X_train.dot(X_train.T)
C = 1
eta1 = 0.01
eta2 = 0.001
n_iter = 1000
H = np.outer(t, t) * K
a = np.ones(n_samples)
for _ in range(n_iter):
grad = 1 - H.dot(a)
a += eta1 * grad
a -= eta2 * a.dot(t) * t
a = np.clip(a, 0, C)
予測
index = a > 1e-8
support_vectors = X_train[index]
support_vector_t = t[index]
support_vector_a = a[index]
term2 = K[index][:, index].dot(support_vector_a * support_vector_t)
b = (support_vector_t - term2).mean()
xx0, xx1 = np.meshgrid(np.linspace(-4, 4, 100), np.linspace(-4, 4, 100))
xx = np.array([xx0, xx1]).reshape(2, -1).T
X_test = xx
y_project = np.ones(len(X_test)) * b
for i in range(len(X_test)):
for a, sv_t, sv in zip(support_vector_a, support_vector_t, support_vectors):
y_project[i] += a * sv_t * sv.dot(X_test[i])
y_pred = np.sign(y_project)
# 訓練データを可視化
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
# サポートベクトルを可視化
plt.scatter(support_vectors[:, 0], support_vectors[:, 1],
s=100, facecolors='none', edgecolors='k')
# 領域を可視化
plt.contourf(xx0, xx1, y_pred.reshape(100, 100), alpha=0.2, levels=np.linspace(0, 1, 3))
# マージンと決定境界を可視化
plt.contour(xx0, xx1, y_project.reshape(100, 100), colors='k',
levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])